20.js树广度、深度遍历

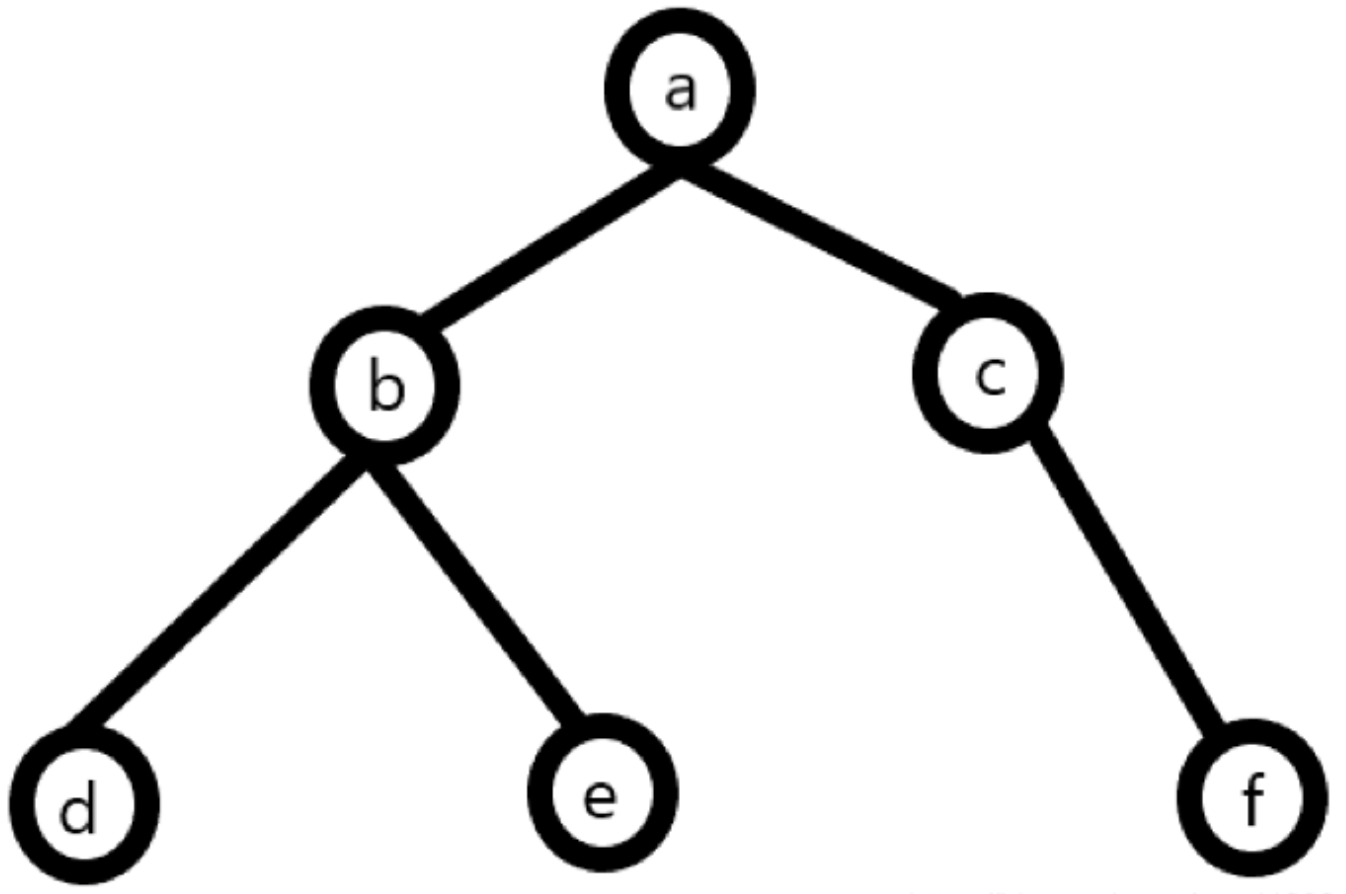
// 先定义一颗简单的树：
let tree = [
    {
      label:'a',
      children:[
          {
              label:'b',
              children:[
                  {
                      label:'d'
                  },
                  {
                      label:'e', // 没有children参数
                  }
              ]
          },
          {
              label:'c',
              children:[
                  {
                      label:'f',
                      children: []  // children参数为空数组【遍历时需要判断没有children，children参数为空数组这两种情况】
                  }
              ]
          }
      ]
    }
]

树的广度优先遍历

广度优先遍历：从上往下对每一层依次访问，对于上面这颗树的遍历顺序为abcdef（此处算法对应到二叉树上，属于先序遍历）

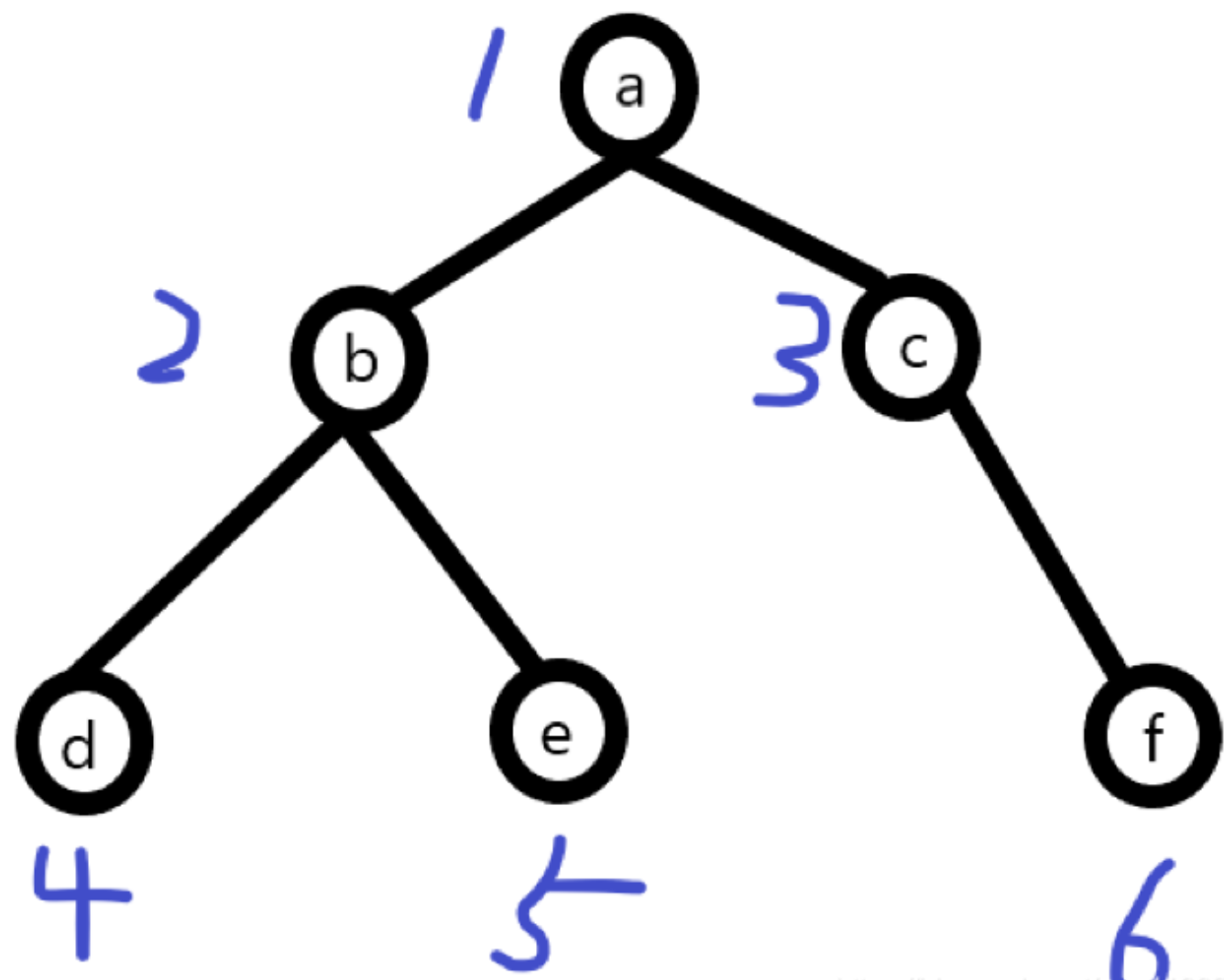
// 方法一：
let bf=function(tree){
    let queue =tree;
    const res = []
    for(let i=0;i<queue.length;i++){
        console.log(queue[i])
        res.push(queue[i].label)
        if(queue[i].children?.length) {queue=queue.concat(queue[i].children)}
    }
    return res
}
console.time('BFS-start')
const result =bf(tree);
console.log(JSON.stringify(result));
console.timeEnd('BFS-start')

// 方法二：
const deepBFS = (root, nodeList = []) => {
  const queue = root;
  // 循环判断队列的长度是否大于0
  while(queue.length > 0) {
      // 取出队列添加的节点
      const p = queue.shift();
      nodeList.push(p.label);
      // 根据节点是否含有children,如果有子节点则添加到队列中
      p.children?.length && p.children.forEach(v => queue.push(v))
  }
  return nodeList;
}
console.time('BFS-start')
const res = deepBFS(tree, []);
console.log(JSON.stringify(res));
console.timeEnd('BFS-start')

树的深度遍历

深度遍历：对每一个可能的分支路径深入到不能再深入为止，对于上面这颗树的遍历顺序为abdecf

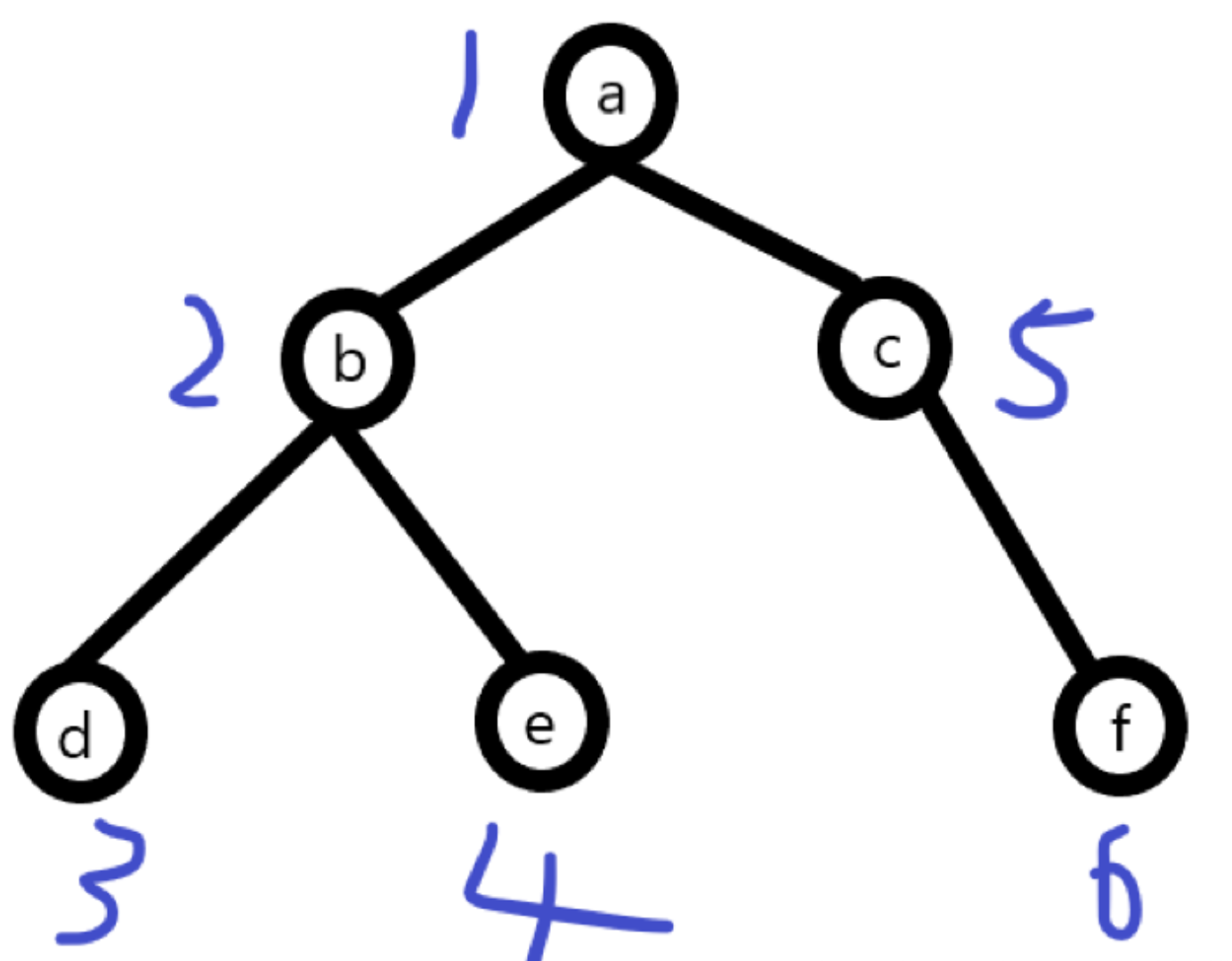
// 方法一：不使用递归
 function dfsHandler(tree, callback) {
    const treeBackup = [...tree];
    const result = []
    
    while(treeBackup.length) {
        const _node = treeBackup.shift();
        result.push(_node.label)
        // 执行遍历回调方法
        typeof callback === 'function' && callback(_node);
        // 存在子节点时将子节点添加到待遍历数据的头部位置
        _node.children && _node.children.length && treeBackup.unshift(..._node.children);
    }

    return result
}

dfsHandler(tree, (val) => {
    console.log('val', val)
})


// 方法二：不使用递归（利用栈的特性）
// 1.创建一个栈（stack）用于保存待访问的节点
// 2.将根节点（node）压入栈中
// 3.进入循环，判断栈是否为空。如果栈不为空，则执行以下步骤：
// -弹出栈顶节点，将其赋值给变量_cur
// -访问当前节点的值，这里使用console.log进行输出，可以根据需要进行相应的处理
// -遍历当前节点的子节点（从右往左），将子节点逆序入栈
// 4.重复步骤3，直到栈为空
const depthFirstSearchIterative = (tree) => {
    const stack = []
    stack.push(tree)
    let _cur = []
    const res = []

    while(stack.length) {
        _cur = stack.pop()
        res.push(_cur.label)
        consle.log('_cur.label', _cur.label)
        for(var i = _cur.children?.length-1; i >= 0; i--) {
            // 判断children是否存在，children存在的话是否为空数组
            if(_cur.children && _cur.children.length) {
                stack.push(_cur.children[i])
            }
        }
    }
    return res
}
depthFirstSearchIterative(tree[0])  // ['a', 'b', 'd', 'e', 'c', 'f']


// 方法三：使用递归
const deepDFS = (root, nodeList = []) => {
  if (root) {
      nodeList.push(root.label);
      // 递归root.children，找root的子节点
      root.children && root.children.forEach(v => deepDFS(v, nodeList))
  }
  return nodeList;
}
const result = deepDFS(root[0], []);

解答下面问题：

想定义一颗tree

const tree = {
  id: 1,
  children: [
    {
      id: 2,
      children: [
        {
          id: 4,
          children: []
        },
        {
          id: 5,
          children: [
            {
              id: 7,
              children: []
            }
          ]
        }
      ]
    },
    {
      id: 3,
      children: [
        {
          id: 6,
          children: [
            {
              id: 8,
              children: []
            }
          ]
        }
      ]
    }
  ]
};

1. 根据当前节点找到他的所有子节点

function findChildNodes(node, targetId) {
  if (node.id === targetId) {
    return node.children;
  }

  for (let i = 0; i < node.children.length; i++) {
    const childNode = node.children[i];
    const result = findChildNodes(childNode, targetId);
    if (result) {
      return result;
    }
  }

  return null;
}
const currentNodeId = 2;
const childNodes = findChildNodes(tree, currentNodeId);

2. 根据子节点向上查找他的所有父级节点

function findParentNodes(tree, targetId, parentNodes = []) {
  if (tree.id === targetId) {
    return parentNodes;
  }

  for (let i = 0; i < tree.children.length; i++) {
    const childNode = tree.children[i];
    const result = findParentNodes(childNode, targetId, [...parentNodes, tree]);
    if (result) {
      return result;
    }
  }

  return null;
}
const currentNodeId = 7;
const parentNodes = findParentNodes(tree, currentNodeId);

3. 根据当前子节点找到和他同级的所有节点

function findSiblingNodes(tree, targetId) {
  const siblingNodes = [];

  // 递归遍历树的函数
  function traverse(node) {
    if (!node || !node.children) {
      return;
    }

    node.children.forEach(child => {
      if (child.id === targetId) {
        siblingNodes.push(...node.children.filter(sibling => sibling.id !== targetId));
        return;
      }

      traverse(child);
    });
  }

  traverse(tree);

  return siblingNodes;
}

const currentNodeId = 5;
const siblingNodes = findSiblingNodes(tree, currentNodeId);

if (siblingNodes.length > 0) {
  console.log("同级节点：", siblingNodes);
} else {
  console.log("未找到指定节点或指定节点没有同级节点");
}